CMU-15-445——P2

目标是实现B+树。

B+树的操作

参考B+ Tree Visualization | B+ Tree Animation (dichchankinh.com)进行可视化操作。B+树存在很多实现方式，本文仅说说我自己的实现。

插入

叶子结点插入与分裂

1. 从根节点开始，找到KV插入的目标叶子结点。
2. 如果该叶子结点满了，则在增加一个新结点放到右边，将左边结点中的一半移动到右边（右边偏多）。并以右边第一个结点作为中间entry向上一级插入。
3. 分裂完后，再根据中间entry决定要插入到左边还是右边。

中间结点的插入与分裂

而对于中间结点，由其子结点向中间结点插入新entry。（这部分的实现是自己想的，可能会存在什么问题）

假设有奇数个entry，再次向上pop的结点选择有三种情况：

1. 插入的entry正好在中间，pop该entry
2. 插入的entry在左边，pop中间靠左的entry，为N / 2
3. 插入的entry在右边，pop中间靠右的entry，为N / 2 + 1

举例：一开始有5个entry（包括第一个空entry），中间的两个为：6，9，我们需要考虑新插入的key不同时，需要向上pop的结点的情况：

X  3   6   9   12         // init

X (1)  3  [6]  9    12    // insert 1
X  3  (4) [6]  9    12    // insert 4

X  3   6  [8]  9    12    // insert 8

X  3   6  [9] (10)  12    // insert 10
X  3   6  [9]  12  (15)   // insert 15

X表示无key元素，最左边的指针；()代表插入的元素，而[]代表需要再次向上pop的元素mid。

其实偶数个entry，与上面奇数的情况相同，不过我们还是再举个例子：

举例：一开始有4个entry，中间的为：6，9

X   3   6   9
X  (1)  3  [6]   9    // insert 1
X   3  (4) [6]   9    // insert 4
X   3   6  [7]   9    // insert 7
X   3   6  [9]  (11)  // insert 11

中间结点插入新entry后，树结构的修改

那么如何构造后续的树的引用关系呢？我们以3个entry举例：

X   3   6
|   |   |
A   B   C

1. 子结点A pop上来一个entry，代表[-inf, 3]需要改成[-inf, 1]以及[1, 3]：

X   3   6          1
|   |   |          |
A   B   C          D

但此时中间结点满了，根据之前的规则，我们需要pop中间靠左的3号：

X   (1)  [3]   6
|    |    |    |
A    D    B    C

目标为：

         X  [3]
        /     \
X   (1)       X    6
|    |        |    | 
A    D        B    C

做法：

1. 根据插入到key，寻找到mid，三选一
2. 如果mid在node中，则从中删除mid，并插入key，并返回mid。
3. 新建页，将其X设置为mid，将node分裂为两个，后半移动到新页。
4. 将mid往上一级插入。其左右分别指向分裂的两个结点。

更多例子

2. 子结点B pop上来一个entry，代表[3, 6]需要改成[3, 4]以及[4, 6]：

X   3   6          4
|   |   |          |
A   B   C          D

根据之前的规则，我们需要pop插入来的4号：

X    3   [4]   6
|    |    |    |
A    B    D    C

目标为：

        X  [4]
       /     \
X    3       X    6
|    |       |    | 
A    B       D    C

3. 子结点C pop上来一个entry，代表[6, +inf]需要改成[6, 8]以及[8, +inf]：

X   3   6          8
|   |   |          |
A   B   C          D

目标为：

        X  [6]
       /     \
X    3       X    8
|    |       |    | 
A    B       C    D

删除

大体思路：

1. 找到删除的叶子结点，进行删除，如果删除完之后，数量大于等于一半，则结束。

2. 如果小于，则需要偷取或者合并。合并时候，需要从上一级中删除某个结点，并且自底向上。

删除比插入更加复杂。推荐PPThttp://courses.cms.caltech.edu/cs122/lectures-wi2018/CS122Lec11.pdf

（再次说明，以下只是我个人的实现方式，B+树有很多种实现方式）

叶子结点的删除

1. 首先找到兄弟结点（parent相同）。有左边选左边，否则选右边（存在优化空间）。（一定存在兄弟结点）

2. 如果兄弟结点的entry数量超过一半，redistribute

   1. 则偷过来一个，要么front，要么back
   2. 并且修改parent结点对应的切分entry
      1. 如果兄弟在左边，则把兄弟的尾偷过来，变成自己的头，修改parent中自己的entry
      2. 如果兄弟在右边，则把兄弟的头偷过来，变成尾，需要修改parent中兄弟的entry

3. 如果兄弟结点也只有一半了，则合并两个结点（例如图中“not”需要合并）

   1. 将所有entry move到兄弟结点中，兄弟在左边，则加到兄弟的尾部，否则加到兄弟的头部

   2. 删除parent结点中的entry：

      1. 如果是兄弟在左边，则删除自己的entry。key与指针，都用兄弟的：

         

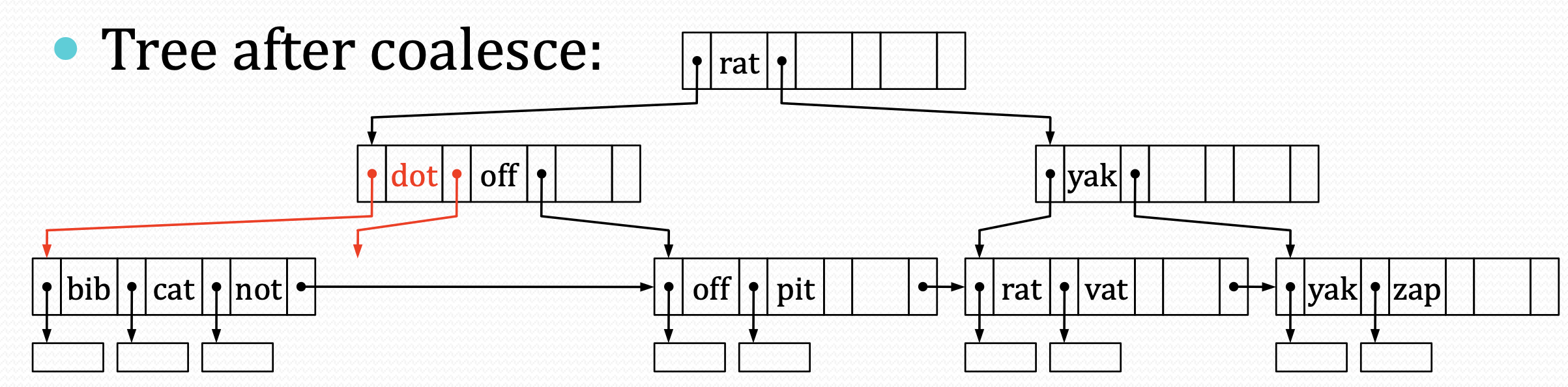
      2. 如果是兄弟在右边，需要用自己的key，但指针还得用兄弟的：

         

   但是实现上来说，当兄弟在右边，则不好实现next指针的修改。因为需要自己的左边的结点的next指向右边的兄弟结点。

   因此，修改第二种情况为：如果兄弟在右边，将兄弟结点的内容移动到自己上，删除兄弟结点。并修改自己的next指向兄弟的next。

中间结点的删除

从子结点过来的删除请求，但是删除之后会导致数量小于一半。

也是要么从兄弟结点偷，要么合并。但是有一点点不同。

1. 先找到兄弟结点。

2. 偷取。过程与叶子结点相同，但是需要考虑parent中的切分entry作为“中继站”：自己从parent拿切分entry，而切分entry则改为从兄弟结点偷的entry。

   

   1. 如果兄弟在左边，则parent中的entry修改为兄弟的尾部，而自己拿到之前parent中的entry。
   2. 兄弟在右边，则parent中的entry修改为兄弟的头部，而自己拿到之前parent中的entry。

   比叶子结点更复杂的地方在于：移动entry时，其指向的page需要改变

   1. 兄弟在左边，具体做法：

      1. 自己头部新增entry：key为切分entry的key，value为自己的X
      2. 将自己的X修改为兄弟的尾部entry的value。需要修改子结点的Parent。
      3. 兄弟pop尾部entry，修改切分entry，key为该pop的entry的key，value为自己结点

   2. 兄弟在右边，简陋图，假设自己是左边的A这个结点：

   

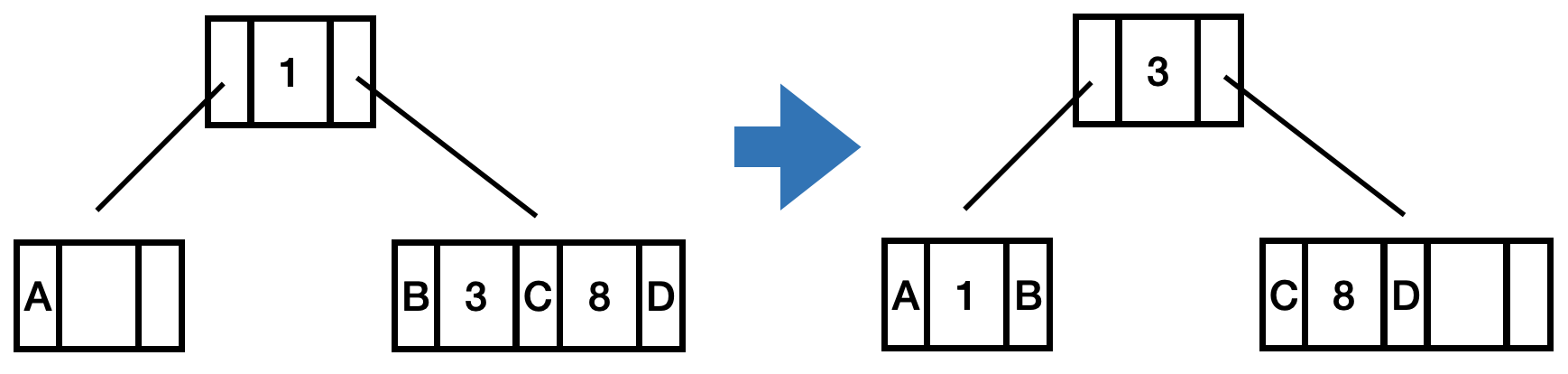
   1. 自己尾部新增Entry，key为切分entry的key，value为兄弟的X。（1，B），修改B的Parent。
   2. pop出兄弟的第1个Entry（3，C），将兄弟的X改为该Entry的Value（C）
   3. 切分的entry的key修改为pop出来的entry的key，value为兄弟结点。

3. 合并。与叶子结点相同，但是同样需要考虑parent结点的切分entry：在先清空自己的entry之前，需要将parent中的entry移动到兄弟上。

   

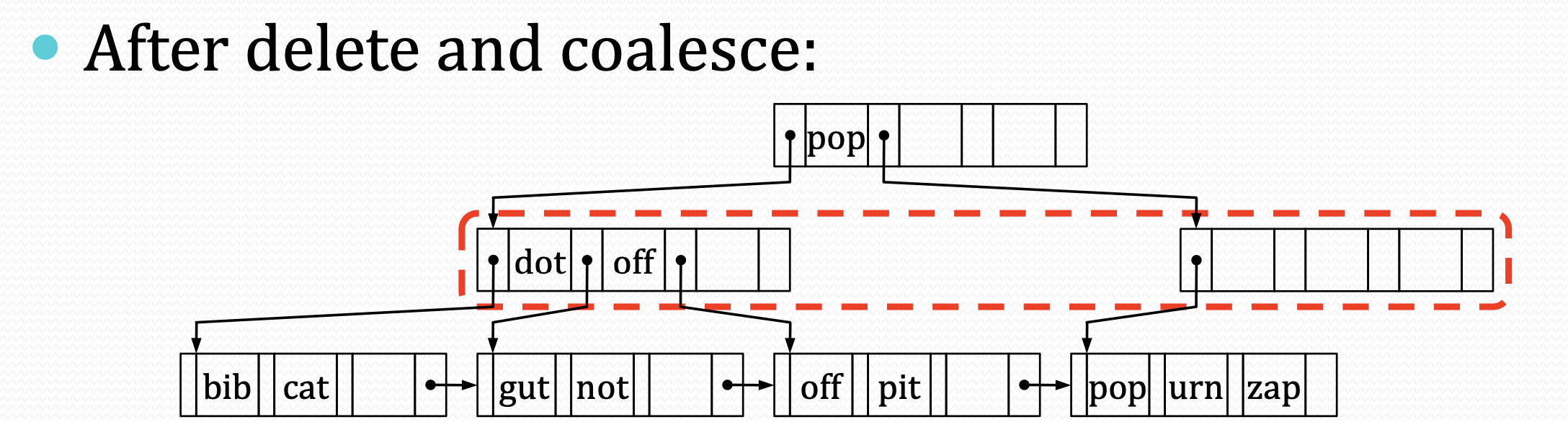
   1. 如果兄弟在左边，则将自己的切分key放到兄弟的尾部。清空自己的entry移动到兄弟尾部。具体来说：
      1. 兄弟新增entry，key为切分entry的key，value为自己的X。修改X的parent
      2. 从头到尾遍历自己的entry，依次添加到兄弟尾部。并修改parent
      3. 从parent中删除自己的entry。
   2. 如果兄弟在右边，则将兄弟的切分key放到兄弟的头部。清空自己的entry移动到兄弟头部。具体与左边相同，不过为了方便，这次将兄弟所有结点放到自己的结点中来。最后同样也是删除自己在parent中的entry。

如果最后删除完entry或者兄弟的entry后，发现parent只有剩下X，也即没有切分entry了，只有一个指向子结点的指针，则可以删除该parent，将B+树的根节点改为其唯一的子结点。

并发控制

目的：

• 避免多线程同时修改某一结点
• 避免一个线程在查询，一个在修改树结构

思路：

1. 拿parent的锁
2. 拿child到锁
3. 如果child是“安全”，释放parent的锁。“安全”指：不会分裂、偷取、合并。也就是不需要修改parent。在插入时，如果结点没满则安全，删除时，entry数量在一半以上则安全。而读锁不需要考虑。

具体：

1. 查询：拿parent锁，再拿child的锁，拿到后释放parent的锁。
2. 插入与删除：从root开始拿，一路到最底下，如果安全则释放除叶子结点外的所有锁。

释放的顺序无所谓，但是从效率考虑，可以自顶向下释放。

优化：

现在的做法导致每次修改操作是互斥的，影响了并发，该优化基于的假设：大部分情况下“安全”，大部分情况只需锁叶子结点就行。因此：

1. 查询：相同
2. 插入与删除：从root开始拿读锁，一路到最底下，叶子拿写锁。如果“安全”，则修改叶子，如果不“安全”则释放所有锁，重新从root开始一路拿写锁。

迭代器的锁：

对树的操作都是自顶向下拿锁，因此不存在死锁。

但是叶子的scan顺序并非自顶向下，因此可能有死锁。

解决：叶子scan不能等待锁，try-lock，失败则释放自己的全部锁，再次重试。

具体实现

这就存在很多方式了，这里说说我的实现，偷懒没实现优化方案。

【存在问题】一种简单但存在问题的释放方式：从叶子到根节点，找parent，释放锁，但有可能插入导致的结构改变，使其不一定还是原来的路径，会导致某些锁无法释放。

可以的做法：记录所有拿的锁，释放的时候依次释放。

【注意】由于在释放锁之前，都不能Unpin（原因是锁依旧在使用中，Unpin可能导致数据变成其他页了，但锁被拿了），因此我们需要将操作中的Unpin改到最后锁释放完了再进行。

在插入操作中，需要考虑的是新建操作，而这些操作在进行时，一定只有该创建的线程在访问，因此可以不带锁，并且用完可以直接Unpin。

在删除操作中，需要考虑到是删除页的时间。我的做法是在调整树结构的过程中，仅记录需要删除的页，而不进行删除（因为锁还被拿着）。等树结构调整完，依次释放一路的锁，然后删除所有需要删除的页。

过程踩坑记录：

有时会出现即便成功修改了parent结点，也反映不到page中。

发现是拿着指针，却unpin了。比如标记哪些page需要删除时，我一开始用的指针来存，然而在调整树结构的过程中，会将那些Page Unpin，于是指针里面就不是需要删除的page了。

即便parent已经被锁了。访问兄弟结点时也需要锁，因为可能该兄弟结点正在被其他线程修改，情况可能是其他线程先拿到锁，并认为兄弟结点的删除safe，因此释放parent锁，然后被当前线程拿到parent的锁了。

Unpin与Delete不对应问题：有时会存在页Unpin数量大于Pin，有时则会出现需要Delete未Unpin完全的页。（目前尚未未解决）

通过测试了，成功垫底。还有很多提升空间，暂时想到两个：兄弟左右的选择，即选择entry数量比较多的兄弟，尽量偷取避免合并，将修改操作改为乐观锁。

其他一些记录

B+树与B树的区别是，B+树中间结点不存具体值，并且最后有一条链。

Leaf中的存储内容

B+树的Leaf结点可以存Record ID，或者直接存储Tuple。例如，Postgres使用前者，而Mysql默认使用后者。

Balance：

• 在多次访问Secondary Index时：前者可以直接拿Record ID去page table访问数据；而后者的Secondary Index存的是Primary Key，还需要再次查询Primary Index拿到值。
• 在多次访问Primary Index时，前者需要每次拿到Record ID后去找page table访问数据；而后者可以直接拿到数据。

我们的实现中，存Record ID。并且没有考虑重复key。

B+树可以压缩，将leaf node中所有结点，自底向上重构B+树，使得空间利用率提升。

Cluster Index保证Sorted，但是不一定保证与Table数据的对应关系。

Mysql保证对应Cluster Index与Table数据的顺序对应。

而Postgres不保证。因为其存的是Record ID，如果要保证对应关系，代价比较大。